いわき市民のヨウ素内部被曝が隠されていたわけ ― 2012/03/14 17:49
いわき市はヨウ素131で汚染された
隠された「福島最大の都市」の初期被曝
『裸のフクシマ』(講談社)に詳しく書いたが、私は3月26日に避難先の川崎市から川内村の自宅に「自主一時帰宅」した。避難が長期化しそうなのと、いつ立ち入りができなくなるか分からないので、重要な荷物などを回収してくることが目的だった。守谷SA:0.33μSv/h。(川崎市の仕事場の倍以上だが、まだまだどうということはない)
日立北IC付近、通過している車の中で1.08μSv/h(このへんはトンネルが続くのだが、トンネルに入ると一気に下がり、0.1~0.5μSv/hくらいに一気に下がる)
関本PA:1.6μSv/h
いわき湯ノ岳PA通過:2μSv/h(時速80kmくらいで走行中の車の中でこれだけ上がった。その後、いわきジャンクションから磐越道に入るところまでは高かったが、磐越道を西に折り返すように進むにつれ、線量はどんどん下がっていった)
差塩PA:0.5μSv/h
小野ICで降りると線量は一気に下がり、町の中では0.3μSv/hくらい(驚くほど低くて拍子抜けした)
……とこんな状況だった。
その後、何度も常磐道を通ったが、他の地域の線量に比べると、いわき市はぐんぐん下がって、数か月後には首都圏とあまり変わらない程度になっていた。
3月下旬のときに高かったのはなんだったのだろうと、ずっと気になっていたのだが、1年経って放送されたNHKのETV特集『ネットワークでつくる放射能汚染地図5 埋もれた初期被ばくを追え』を見てその謎が解けた。
セシウムとヨウ素では、汚染地帯が正反対だったというのだ。
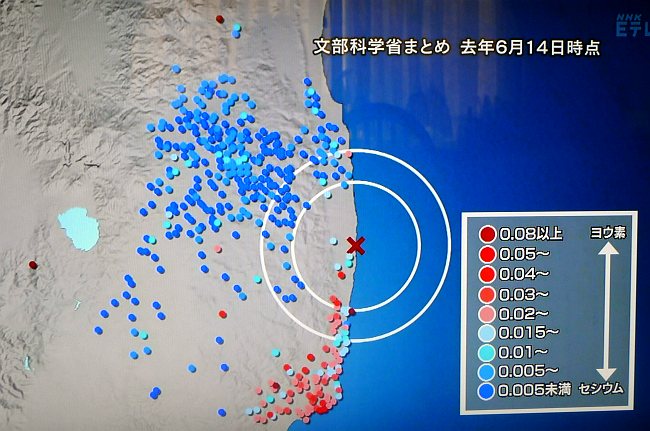
↑青いのがセシウム、赤いのがヨウ素131
これは文科省データだけで証明できている。ただ、文科省データは別々に計測地点と数値だけを出しているから、このようにきれいに可視化されず、気がつく人は少なかった。
番組では、独立行政法人海洋研究開発機構の2人の研究者などがまとめたヨウ素131の拡散状況が公開されていた。
いわき市を通過して茨城、栃木、群馬方向に流れていったという。
セシウムとヨウ素の拡散状況がこれだけ違ったのは、放出時期とそのときの風向きによるものだろう。あのとき、風は大半が東に、つまり海側に流れていったので、放射性物質もほとんどが太平洋に流れていってくれたが、ちょっと風向きが変わっていただけで首都圏が飯舘村並みに汚染されていた可能性もあるのだ。
で、問題はいわき市などに降ったヨウ素131による内部被曝だ。
ヨウ素131は半減期が8日だから、もはや痕跡は残っていない。今からホールボディカウンターを使ったところで出ない。
空中を流れていったのだから、風下にいた人たちは微粒子ごと体内に吸い込んでいる。
その初期被曝でどれだけ健康に問題が出るのかは分からない。ヨウ素の放射能がすでに消えてしまっているのだから、今からできることはない。
1年前にDNAが壊されたとすれば、その後の自然修復に期待するしかない。
いわき市は今はもうほとんど汚染されていないと言ってもいいので、今から避難してもあまり意味はないだろう。くよくよせず前向きに行動し、栄養のあるものを食べて、よく眠り、傷ついたDNAを修復することがいちばんかと思う。
いわき市民に避難地区と同レベルの「精神的損害補償」を支払うと4000億円/年
いわき市は福島県最大の都市だから、ここでシビアなヨウ素131被曝があったと認めてしまうと、賠償問題などが今とは桁違いに膨れあがる。避難していた精神的障害への賠償という名目で避難区域の人たちには10万円/月が支払われているが、同様にいわき市の人たちに、「状況を知らされないまま初期被曝をさせられ、その恐怖を今後ずっと抱え続けることへの精神的障害」への賠償を行ったらどれくらいの金額になるのだろうか。
いわき市の人口は約34万人。避難地域並みに1人10万円/月の「精神的損害補償」を支払ったら、ひと月で340億円。1年で4000億円を超える。
当然、セシウム汚染がひどかった福島市や郡山市など、中通りの人たちの精神的苦痛も無視できないから、その人たちにも全員10万円/月を支払えば、軽く兆を超える賠償金が必要になる。
福島県全体なら約200万人だから、月に2000億円、年2兆4000億円……。
だから国も東電もひたすら都市部の汚染には目を向けないようにさせているのだろう。
都市部の汚染は数値的に明らかなのに、国民やマスコミの目を都市部よりも原発周辺の過疎地に向けることで、賠償問題が大きくなることを防ごうとしている。
せめて今からできることは、これから出てくるかもしれない子供の甲状腺癌の兆候を見逃さないようにしっかり見守る態勢を作ること。兆候が出たらすぐにできうる限りのケアを施せるように準備すること。せめてそのくらいはしっかりやってもらわないと。

青がセシウム汚染、赤がヨウ素131汚染。はっきり分かれている

(独)海洋研究開発機構の研究者がまとめたヨウ素131の流れ
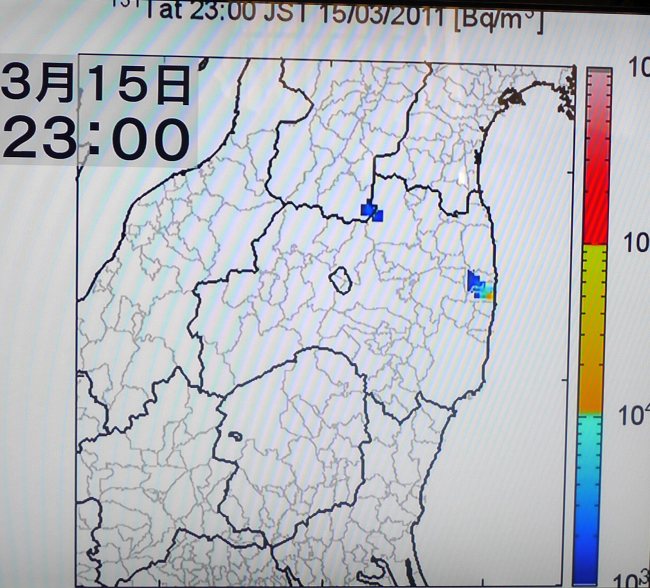
ヨウ素131の拡散シミュレーション(1)
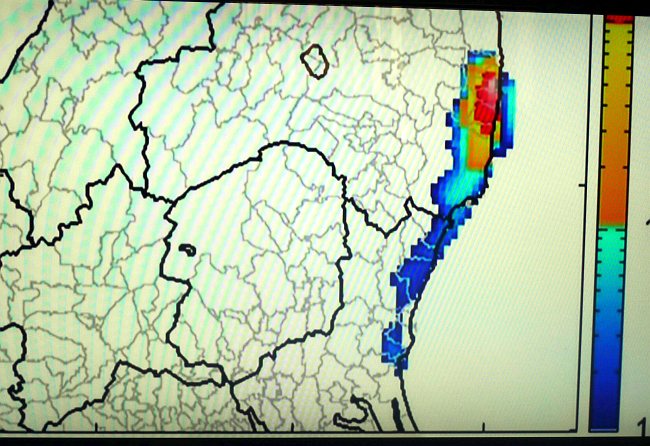
その2 まず南方向に流れ出した
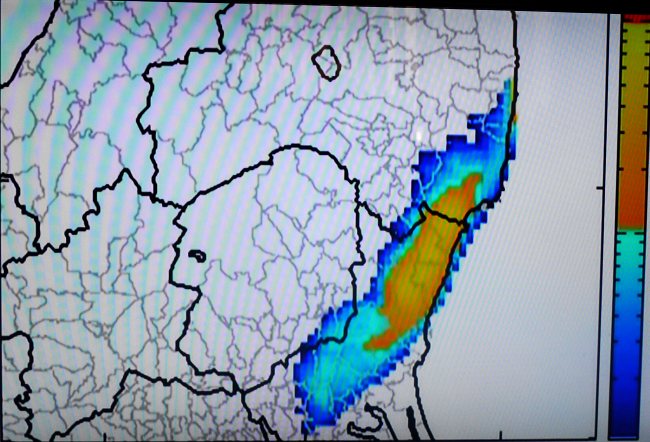
その3 いわき市を直撃してさらに南へ
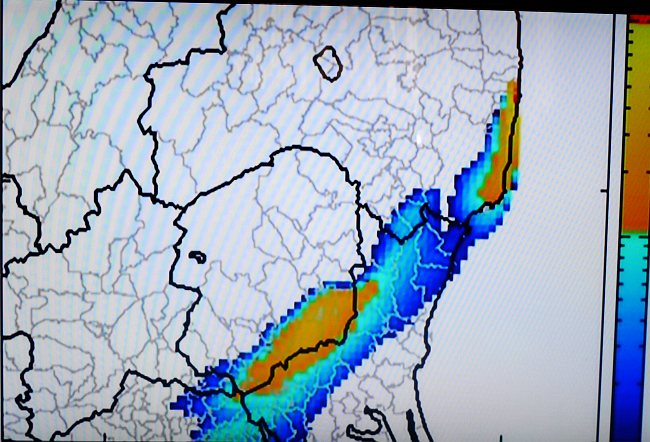
風が東寄りに代わり、茨城・栃木へ
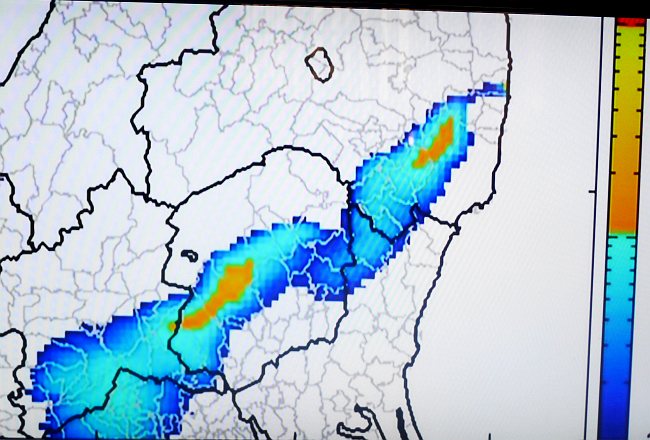
宇都宮あたりもヨウ素131はかなり飛んできた
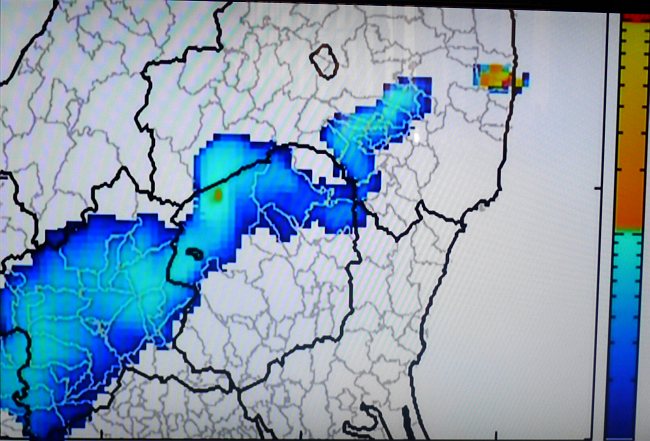
日光や南会津もかなりやられた。そして群馬に……
※いずれもNHK 『ETV特集 ネットワークでつくる放射能汚染地図5 埋もれた初期被ばくを追え』 より
東電品川火力が福島第一だったら ― 2012/03/20 13:56
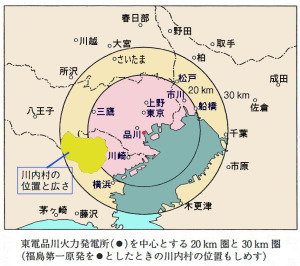
もしも東電品川火力発電所が福島第一原発だったら
23区内はすべて立ち入り禁止、横浜、さいたま、千葉も生活不能
前にも出したが、「もしも東電品川火力発電所が福島第一原発だったら」という地図の分かりやすいやつがようやくできたので公開したい。(上の図 クリックで拡大)
4月20日に出版する『3.11後を生きるきみたちへ 福島からのメッセージ』(岩波ジュニア新書)の冒頭で使うために岩波の編集部に作っていただいたものを元に着色した。
3.11後1年以上経った今でも、事故原発20km圏内は立ち入り禁止の「警戒区域」で、入ると罰せられる。
30km圏では学校や病院が再開できていないから、事実上生活ができない。
また、30km圏までの住民には、「避難中の精神的損害補償」として1人あたり10万円/月の賠償金が支払われているが、これを首都圏でやったら完全に日本は破産する。
ざっと2000万人が該当するとして、1年で、これだけで24兆円なのだから。
★3月24日の富士見市の講演会用に項目まとめを作ったので、それも併せて公開。
まだ空きはたくさんあるそうです。申し込みは
tel:049-261-5371 (ふじみ野交流センター)までお願いします。
■ あの日何が起きたのか + 最近分かったこと
●もしも1Fが東電品川火力の位置だったら……富士見市は最も汚染された津島の位置
●絶対に停電してはいけない場所でのお粗末すぎる備え
●津波が来る前に壊滅状態……2Fは今でも相当ひどい
●見捨てられた人たち・見捨てた人たち……県は国より先に知っていた
●徹底して隠された汚染の事実……ヨウ素131は南に流れていた
●最も危険な場所に避難誘導された……津島で何が起きていたか
●川内村全村避難劇の裏側……東電と富岡町長は最後まで避難を渋った
●線量計で汚染状況をいち早く検証……最初に情報が流れたのはmixi
■ 放射能とつき合うしかなくなった
●放射能汚染の基礎知識……ベータ線、アルファ線源はほとんど検査していないという実情
●外部被曝と内部被曝……怖いのは内部被曝
●テレビが放射能被害を拡大させた……警戒すべきときに安全といい、安全になってから煽る
●放射能とどこまで「共存」できるのか……福島の農家、さまざまなスタンス
■ 壊されたコミュニティ
●わざわざ線量の高い学校に通わされた子供たち
●30km圏の我が家に帰ったときの気持ちとその後の展開
●テレビで伝えられる映像とのギャップ
●義援金はどこにどう渡ったのか……津波被害地域にもっと配るべき
●家に戻ると補償金がもらえない……「帰れない」の本当の理由
●同じ福島県民同士がいがみ合う……飲み屋、パチンコ屋、タクシーは儲かるけれど
●汚染していないコメを捨てさせる……農家から誇りや生き甲斐を奪うことの怖ろしさ
■ 放射能より怖いもの
●「除染」によって危険が広がることもある……除染は単純な正義ではない
●森の除染は「儲かる」……優先順位もやり方もおかしい
●除染作業は内部被曝が心配……わざわざ再拡散~粉塵を吸い込んで内部被曝
●「国策」に潜む大きな危険……税金投入がなければそもそも原発はなかった
●命にとって本当の「危険」とは……生き甲斐、楽しさのない人生こそ危険
■ これからの時代の「自治力」「地域力」
●中越地震が教えてくれたこと……土地に根ざして生きることの大切さ
●永遠に成長し続けることはできない……石油が涸渇すれば「自然エネルギー」も使えない
●価値観の多様な世界に生きたい……マイナス成長時代を楽しむ
●「田舎で起業」「熟年王国建設」の勧め……発想を変えて生き抜く工夫。本当に住みたい土地、住みやすい町とは?
『フクシマの嘘』ドイツZDFの30分番組 ― 2012/03/21 16:31
長野県県立高校入試問題数学の問題はよい問題 ― 2012/03/30 16:18
放射能問題ばかり続いて、このブログも内容的にかなり辛くなってきたので、ここでちょっと頭の体操というか、息抜きの話題をひとつ。
こんな算数?の問題。
問1 「周囲が12cmの丸い蓋があります。この縁のスタート地点Aからアリが毎秒2cmの速さで蓋の周縁をぐるっと回り、10秒後に止まりました。この10秒の間に、出発点から直線距離でいちばん離れた地点(蓋を隔ててちょうど正面の地点)を2回通過しました。2回目に正面地点に来たのは何秒後で、そのとき何cm動いたことになるでしょうか?」
……図にするとこんな感じ↓

簡単ですよね?
円周が12cmで、秒速2cmで動くのだから、1周は6秒。正面の位置(時計の6時地点から見れば12時の位置)に来るのは半分の6cmだから3秒後と9秒後ですね。
では次の問題。
問2 「今のアリの動きをグラフで表すと下図のようになります。y は進んだ距離(cm)、x は経過時間(秒)です。このグラフ上で、アリが2回目に出発点からいちばん離れた地点(正面地点)を通過するときの時間と進んだ道のりを表す点の座標を求めなさい」
こういうことですね↓(赤い点線が2回目に出発点の正面に来るポイントを表している)

中学生になると、算数から数学というものに変わるんですが、多くの場合、数学教師が算数と数学の違い、考え方の違いをきちんと教えないまま、ただ教科書に出てくる例題を解いて見せて、丸暗記させるということをします。その結果、一気に数学嫌いの生徒が増えます。
数学は代数と幾何に大別できますが、代数の考え方というのは、文字通り「数」の代理をさせる言葉を学ぶというか、数学という言語の文法を教えるものだと僕は思っています。
定数とか変数という概念。式の中に数を「代入する」という方法論。
上の問2は、小学生までに習っていた算数とは違う世界にこれから入っていきますよ、という、優しいオリエンテーションのような問題ですね。
中学に行って最初に習った代数が一次関数でした。
y=ax あるいは y=ax+b という式で表せる、斜めに一直線に伸びるグラフと一緒に学んだあれ。
こんな基本的なことさえも、今の僕は忘れていますが、これを書きながら少し思い出してきました。
で、平面の座標というのは、x軸とy軸の二次元で表せる、なんてことも一緒に学びました。
今までは「ここから東の方向に200mくらいのところかなあ」なんていう言い方しかできなかったのを、「この地点をx,y=0 として、北がy,東がx、単位をmとすれば、x=202,y=3の地点」なんて言い方ができるようになる。これも、算数から数学に進んだ証だったわけですね。
この問題はそれを思い出させているような問題。
答えは「9秒後に6mの位置」なので、 x=9,y=6 です。
問3 「上の図で、xが6以上10以下のとき、つまりアリが2周目に入って10秒後に止まるまでの間のy(スタート地点からの道のり)をx(スタートしてからの時間)で表しなさい」
どんどん数学っぽく?なってきました。
アリは毎秒2cmで動いているので、動いた道のり(y cm)と時間(x 秒)は y=2x で表せます。
ただし、円周上を回っていて、y(出発点からの道のり)は元に戻るとゼロリセットするということなので、6秒でゼロに戻されます。だから、2周目に入ったときのy(出発点からの道のり)は、x(時間)から6秒の分を引けばいい。
つまり、xを「x-6」にすれば2周目の式になります。毎秒2cmは変わらないから、xの代わりに(x-6)を入れて y=2(x-6) 。カッコを外すと、y=2x-12 ですね。
……数学をすっかり忘れている僕も、このへんまではなんとなく思い出せました。
問題はさらに続きます。
問4 問1のアリと同時に、同じ場所からテントウムシがアリとは逆方向に毎秒3cmの速さで動き始め、アリと同じように10秒後に止まりました。このとき、テントウムシが周回して出発点に戻ってくるまでの「残りの道のり」を y とします。例えば、1秒後には 3cm 進んでいて、残りは 12-3 で 9cm ですから、x=1 のとき、y=9 です。
図で表せばこんな感じですね↓

さて、このとき、テントウムシの1周目、つまりテントウムシがスタートして4秒後までの間の、yとxの関係式を表しなさい。
これも簡単ですね。y はさっきのアリとは違って、出発点からの道のりではなくて、出発点に戻るまでの残りの道のりですから「12-3x」です。y=12-3x をきれいにして、答えは y=-3x+12
よく覚えていないのですが、確か、y=ax+b という形が一次関数の基本だったような……。だから、これが美しい形で書いた答えでしょう。
問5 「アリとテントウムシは10秒後に止まるまでに4回すれ違います。4回目にすれ違うのは出発して何秒後でしょうか」
小学校でやった(今はやらないのかも?)「旅人算」の一種ですね。
A地点とB地点を互いの出発点に向かって同時に出発した太郎と花子が何秒後にすれ違うか、という問題。ここではさらに凝っていて、太郎も花子も、相手が出発した場所まで行ったらそのまま戻ってくるという往復運動を続ける……と。
円周上を逆方向に回る二人がすれ違うというのは、直線上を行ったり来たりしている二人がすれ違うのと似ています。すれ違う場所はちがってきますが、すれ違う時間ポイントは同じ。
でも、こういうのを算数で考えるととてもやっかいなので、数学(この場合は一次関数)という便利な方法でやれば簡単ですよ……ということを教えている問題ですね、これは。
さて、この問題では、アリもテントウムシも10秒後には止まります。
アリは最初に見たように、1周6秒なので、10秒で1周と3分の2動きます。テントウムシは1周4秒なので、10秒で2周半するわけです。
で、「すれ違う」というのはどういうことかというと、アリにとっての出発点からの道のりと、テントウムシにとっての出発点までの残りの道のりが一致したとき、ということだと気がつきます。
それを気づかせるために、わざわざ1つ前の問題で「テントウムシが周回して出発点に戻ってくるまでの残りの道のりを y とします」というのが出てくるではないですか。嬉しいヒントがあったんですね。出題者はとっても親切な人のようです。
テントウムシにとっての「残りの道のり」は、逆方向に進んでいるアリにとっては進んでいる道のりだから、これが一致するときがすれ違うときになります。
これをグラフで表すと、こんな感じになります↓

黒の直線がアリで、緑の線がテントウムシです。これらが交わる点(ピンクの○で囲った点)でアリとテントウムシはすれ違うわけです。
グラフにすると、なるほど、確かに10秒後に両方が止まるまでの間に4回すれ違うことになっています。
文系の僕としては、いきなり4回目を考えるのは怖いので、1回目から順番に見ていきます。
テントウムシが最初に1周するまでにアリとすれ違う時間を考えると、この前の設問で出した y=-3x+12(テントウムシ) と アリの y=2x を並べて、yが一致したときのxが答えになるはずです。
-3x+12=2x だから、5x=12 x=12/5 つまり2.4秒後に最初にすれ違う……と。
次は2回目。
グラフを見ても分かるように、テントウムシの2回目の出発点は4秒後で、そこから最初と同じ下降線を描きます。この線をy軸まで伸ばしていくと12の2倍の24のところで交わるはずですから(上の三角形が相似形なので)、式を書くなら、
y=-3x+24 でしょうか。
これと1回目のy=2x(アリ)をイコールで結ぶと、2x=-3x+24 5x=24 x=24/5 で、4.8秒後だ~、っと。
次、3回目。
テントウムシはまだ2周目の途中で、今の y=-3x+24 のまま。しかし、アリは1周終えてゼロリセットされています。最初の設問で問われた6秒後から10秒で止まるまでのアリの式は y=2x-12 でした。これをイコールで結ぶから、-3x+24=2x-12 ⇒ 36=5x ⇒ x=36/5 で、7.2秒後です。
いよいよ4回目。
テントウムシは3周目に入っています。y=-3x+36 ですね。アリは変わらず2周目です。y=2x-12。これをイコールで結んで、2x-12=-3x+36 ⇒ 5x=48 ⇒ x=48/5 で、9.6秒後。
……ほんとかしらと、グラフと照合してみると、大体全部合っていそうです。多分、合っているだろう……というのが文系人間の僕が精一杯考えた解答であります。
問6 「アリが出発してから7秒後にテントウムシとすれ違うためには、テントウムシは秒速何cmで動けばいいですか」
テントウムシが秒速3秒で動いたとき、7.2秒後に3回目のすれ違いをすることはすでに計算済みです。これを7秒後に修正すればよさそうですから、やはり3回目のすれ違いでしょう。
すれ違い3回目の式は、アリは y=2x-12 でした。テントウムシは y=-3x+24 でした。
この 「3x」の 3(毎秒3cmの3)をa(毎秒a cm)にして、x(経過時間)が7(秒)になるときのa(秒速)を出せばいいわけです。
そのように代入すると、14-12=-7a+24 ⇒ -7a=-22 a=22/7 小数にすると、3.1428571428571428571428571428571 ……ほぼ円周率に同じ。
おお~、ちょっとお洒落な答えですね。
……以上が、今年長野県の県立高校入試数学で出題された問題の一部を、言い方を変えて表したものです。
元の問題は冒頭の図のようになっていますが、よく読むと、この問題は円柱など必要なく、また「平行になる」は、「この円柱を真上から見たときに2点が重なる、一致するということと同じ」であることはすぐに分かります。
円柱も平行も一種の「引っかけ」というか、数学的な表現に変換されているだけで、基本は時計算とか旅人算。つまり、「数学的な表現」を読み解けば、ここに書いたような小学生の算数の問題になるわけです。
算数で解こうとすれば難しいのですが、数学の基礎をちゃんと学び取っていれば、誰でも解ける問題です。(問題量が多すぎてじっくり解いている時間がない、というような批判は別。全体の問題量が適切かまでは見ていません。あくまでもこの問題が難しすぎるのかどうかということだけを考察しています)
簡単に言える内容なのに、わざわざ円柱だの平行だのという言い方に変えているのは難問奇問を作為的に作っていてけしからん、という批判が出るかもしれません。しかし、それは「数学的表現とはどういうものか」という基本的なことを学んでいるかどうかを見るにはとてもいい方法です。
例えば、将来、何かの装置を作るとき、このような円筒状の両端で逆方向に違う速度で回るベアリングとか歯車とかの設計をすることがあるかもしれません。そのとき、計算上、円柱を考える必要はないのだ、と分かるかどうかというのはものすごく基本的なことで、技術者や設計者に問われる基礎力です。
そんなことも気がつかないような頭の人に、重要な装置や機械を設計し、運用させることはできません。
ここで話を放射能事故に戻します。
東電や保安院の記者会見を見ていて、多くの人は「この人たちって、難しい入試を突破して、偏差値の高い大学に入って、優秀な成績で卒業してこの仕事に就いたんでしょうに、なんでこんなにバカなのかしら」と不思議に思ったに違いありません。
昨日、たまたまフェイスブックで「長野県の県立高校入試問題における数学の問題が超難問で、受験生が泣いている」という話題を見つけたのですが、すでにネット上では、教科書に載っていないようなこんな難問を出すべきではないという論がたくさん書き込まれているようです。
あげくは、 //県教組では、現行の学習指導要領を逸脱していると判断し、15日になって県教委に抗議し、外部評価を行うよう申し入れた// なんて記事まで出てきました。
バッカじゃなかろか。
そんなとんでもない問題ではないことは、ここに説明したとおり。むしろこれは、 y=ax+b という一次関数の基本さえ理解していれば誰でも解ける「いい問題」なのです。しかも、「数学的表現」を一般的な意味合いに読み替えて直観的に把握する能力も問われています。
この問題を評して「数学の問題というよりは国語の問題」と言っている人がいましたが、ある意味そうかもしれません。
つまり、数学とはどういう学問なのか、その「精神」を知らせることが本当の教育ではないのか、というテーマを表現しているのですね。
数学って、一見難しいように思えても、噛み砕いて考えればどうということのないことも多いんだよ。しかも、一度数式を作ってしまうと後はあてはめるだけで簡単に答えが出てくるから便利なんだよ、ということを教えている。
しっかりした教育哲学を持った人が作った問題だと思います。
数学が苦手な生徒でも、頭を使えば必ず解けるということがすごく重要です。その意味において、この問題はとてもいい問題なのです。
ちなみに僕は高校生ですでに数学を捨ててしまい、大学は数学が入試科目にない私立文系のみを受けました。
実は、この問題を解いているときも、y=ax+b なんて忘れていたし、このaがマイナスになるとグラフが右下がりのグラフになるという超基本的なことさえすっかり忘れていました。問題を解きながら、そういえばそんなことを教わっていた気がするなあ……という程度の記憶がゆるやかに甦ってきてちょっと嬉しくなったりもしました。理系の人からはバカにされそうですが、ほんとにそれほどひどい落ちこぼれなのです。
そんな僕でさえ、考えれば解けるのですから、ましてや現役で数学を学んでいた中学生が解けないはずはありません。
教科書の例題を丸暗記して定期試験で点を取るタイプの生徒、定期試験の点を取る要領だけを身につけた生徒は面食らうかもしれません。しかし、そういう生徒、「想定内の問題だけ勉強すればいい」という根性の生徒が点を取れるようなパターン化した試験問題こそ、官僚バカ、学者バカ、バカ政治家たちを量産する、悪い試験問題といえるでしょう。
頭の使い方を鍛えないで、「想定外でした」なんていう嘘を平気でつくような図太さだけは身につける。日本の将来を背負う子供たちが、そんな大人に育っていくのではたまったものではありません。
この問題を見て、考える前に泣き出すだとか、この後の科目を投げちゃうなんていうのは、数学以前に、人間の芯の強さとか、根性とかが足りないわけで、それもまた問題だと思います。
入試を楽しむくらいの力量、余裕を持ってくれよ。これから先の人生、いっぱい大変なことがあるんだから、この程度のことでめげてたらやっていけないよ、と言いたいのです。
……あ~、何十年ぶりかで数学のエッセンスを楽しませてもらった気分です。この問題の作者に感謝!
もしかして、この問題の作者は、ヤマゲン先生みたいな人かもしれないなあ。
こんな算数?の問題。
問1 「周囲が12cmの丸い蓋があります。この縁のスタート地点Aからアリが毎秒2cmの速さで蓋の周縁をぐるっと回り、10秒後に止まりました。この10秒の間に、出発点から直線距離でいちばん離れた地点(蓋を隔ててちょうど正面の地点)を2回通過しました。2回目に正面地点に来たのは何秒後で、そのとき何cm動いたことになるでしょうか?」
……図にするとこんな感じ↓

簡単ですよね?
円周が12cmで、秒速2cmで動くのだから、1周は6秒。正面の位置(時計の6時地点から見れば12時の位置)に来るのは半分の6cmだから3秒後と9秒後ですね。
では次の問題。
問2 「今のアリの動きをグラフで表すと下図のようになります。y は進んだ距離(cm)、x は経過時間(秒)です。このグラフ上で、アリが2回目に出発点からいちばん離れた地点(正面地点)を通過するときの時間と進んだ道のりを表す点の座標を求めなさい」
こういうことですね↓(赤い点線が2回目に出発点の正面に来るポイントを表している)

中学生になると、算数から数学というものに変わるんですが、多くの場合、数学教師が算数と数学の違い、考え方の違いをきちんと教えないまま、ただ教科書に出てくる例題を解いて見せて、丸暗記させるということをします。その結果、一気に数学嫌いの生徒が増えます。
数学は代数と幾何に大別できますが、代数の考え方というのは、文字通り「数」の代理をさせる言葉を学ぶというか、数学という言語の文法を教えるものだと僕は思っています。
定数とか変数という概念。式の中に数を「代入する」という方法論。
上の問2は、小学生までに習っていた算数とは違う世界にこれから入っていきますよ、という、優しいオリエンテーションのような問題ですね。
中学に行って最初に習った代数が一次関数でした。
y=ax あるいは y=ax+b という式で表せる、斜めに一直線に伸びるグラフと一緒に学んだあれ。
こんな基本的なことさえも、今の僕は忘れていますが、これを書きながら少し思い出してきました。
で、平面の座標というのは、x軸とy軸の二次元で表せる、なんてことも一緒に学びました。
今までは「ここから東の方向に200mくらいのところかなあ」なんていう言い方しかできなかったのを、「この地点をx,y=0 として、北がy,東がx、単位をmとすれば、x=202,y=3の地点」なんて言い方ができるようになる。これも、算数から数学に進んだ証だったわけですね。
この問題はそれを思い出させているような問題。
答えは「9秒後に6mの位置」なので、 x=9,y=6 です。
問3 「上の図で、xが6以上10以下のとき、つまりアリが2周目に入って10秒後に止まるまでの間のy(スタート地点からの道のり)をx(スタートしてからの時間)で表しなさい」
どんどん数学っぽく?なってきました。
アリは毎秒2cmで動いているので、動いた道のり(y cm)と時間(x 秒)は y=2x で表せます。
ただし、円周上を回っていて、y(出発点からの道のり)は元に戻るとゼロリセットするということなので、6秒でゼロに戻されます。だから、2周目に入ったときのy(出発点からの道のり)は、x(時間)から6秒の分を引けばいい。
つまり、xを「x-6」にすれば2周目の式になります。毎秒2cmは変わらないから、xの代わりに(x-6)を入れて y=2(x-6) 。カッコを外すと、y=2x-12 ですね。
……数学をすっかり忘れている僕も、このへんまではなんとなく思い出せました。
問題はさらに続きます。
問4 問1のアリと同時に、同じ場所からテントウムシがアリとは逆方向に毎秒3cmの速さで動き始め、アリと同じように10秒後に止まりました。このとき、テントウムシが周回して出発点に戻ってくるまでの「残りの道のり」を y とします。例えば、1秒後には 3cm 進んでいて、残りは 12-3 で 9cm ですから、x=1 のとき、y=9 です。
図で表せばこんな感じですね↓

さて、このとき、テントウムシの1周目、つまりテントウムシがスタートして4秒後までの間の、yとxの関係式を表しなさい。
これも簡単ですね。y はさっきのアリとは違って、出発点からの道のりではなくて、出発点に戻るまでの残りの道のりですから「12-3x」です。y=12-3x をきれいにして、答えは y=-3x+12
よく覚えていないのですが、確か、y=ax+b という形が一次関数の基本だったような……。だから、これが美しい形で書いた答えでしょう。
問5 「アリとテントウムシは10秒後に止まるまでに4回すれ違います。4回目にすれ違うのは出発して何秒後でしょうか」
小学校でやった(今はやらないのかも?)「旅人算」の一種ですね。
A地点とB地点を互いの出発点に向かって同時に出発した太郎と花子が何秒後にすれ違うか、という問題。ここではさらに凝っていて、太郎も花子も、相手が出発した場所まで行ったらそのまま戻ってくるという往復運動を続ける……と。
円周上を逆方向に回る二人がすれ違うというのは、直線上を行ったり来たりしている二人がすれ違うのと似ています。すれ違う場所はちがってきますが、すれ違う時間ポイントは同じ。
でも、こういうのを算数で考えるととてもやっかいなので、数学(この場合は一次関数)という便利な方法でやれば簡単ですよ……ということを教えている問題ですね、これは。
さて、この問題では、アリもテントウムシも10秒後には止まります。
アリは最初に見たように、1周6秒なので、10秒で1周と3分の2動きます。テントウムシは1周4秒なので、10秒で2周半するわけです。
で、「すれ違う」というのはどういうことかというと、アリにとっての出発点からの道のりと、テントウムシにとっての出発点までの残りの道のりが一致したとき、ということだと気がつきます。
それを気づかせるために、わざわざ1つ前の問題で「テントウムシが周回して出発点に戻ってくるまでの残りの道のりを y とします」というのが出てくるではないですか。嬉しいヒントがあったんですね。出題者はとっても親切な人のようです。
テントウムシにとっての「残りの道のり」は、逆方向に進んでいるアリにとっては進んでいる道のりだから、これが一致するときがすれ違うときになります。
これをグラフで表すと、こんな感じになります↓

黒の直線がアリで、緑の線がテントウムシです。これらが交わる点(ピンクの○で囲った点)でアリとテントウムシはすれ違うわけです。
グラフにすると、なるほど、確かに10秒後に両方が止まるまでの間に4回すれ違うことになっています。
文系の僕としては、いきなり4回目を考えるのは怖いので、1回目から順番に見ていきます。
テントウムシが最初に1周するまでにアリとすれ違う時間を考えると、この前の設問で出した y=-3x+12(テントウムシ) と アリの y=2x を並べて、yが一致したときのxが答えになるはずです。
-3x+12=2x だから、5x=12 x=12/5 つまり2.4秒後に最初にすれ違う……と。
次は2回目。
グラフを見ても分かるように、テントウムシの2回目の出発点は4秒後で、そこから最初と同じ下降線を描きます。この線をy軸まで伸ばしていくと12の2倍の24のところで交わるはずですから(上の三角形が相似形なので)、式を書くなら、
y=-3x+24 でしょうか。
これと1回目のy=2x(アリ)をイコールで結ぶと、2x=-3x+24 5x=24 x=24/5 で、4.8秒後だ~、っと。
次、3回目。
テントウムシはまだ2周目の途中で、今の y=-3x+24 のまま。しかし、アリは1周終えてゼロリセットされています。最初の設問で問われた6秒後から10秒で止まるまでのアリの式は y=2x-12 でした。これをイコールで結ぶから、-3x+24=2x-12 ⇒ 36=5x ⇒ x=36/5 で、7.2秒後です。
いよいよ4回目。
テントウムシは3周目に入っています。y=-3x+36 ですね。アリは変わらず2周目です。y=2x-12。これをイコールで結んで、2x-12=-3x+36 ⇒ 5x=48 ⇒ x=48/5 で、9.6秒後。
……ほんとかしらと、グラフと照合してみると、大体全部合っていそうです。多分、合っているだろう……というのが文系人間の僕が精一杯考えた解答であります。
問6 「アリが出発してから7秒後にテントウムシとすれ違うためには、テントウムシは秒速何cmで動けばいいですか」
テントウムシが秒速3秒で動いたとき、7.2秒後に3回目のすれ違いをすることはすでに計算済みです。これを7秒後に修正すればよさそうですから、やはり3回目のすれ違いでしょう。
すれ違い3回目の式は、アリは y=2x-12 でした。テントウムシは y=-3x+24 でした。
この 「3x」の 3(毎秒3cmの3)をa(毎秒a cm)にして、x(経過時間)が7(秒)になるときのa(秒速)を出せばいいわけです。
そのように代入すると、14-12=-7a+24 ⇒ -7a=-22 a=22/7 小数にすると、3.1428571428571428571428571428571 ……ほぼ円周率に同じ。
おお~、ちょっとお洒落な答えですね。
……以上が、今年長野県の県立高校入試数学で出題された問題の一部を、言い方を変えて表したものです。
元の問題は冒頭の図のようになっていますが、よく読むと、この問題は円柱など必要なく、また「平行になる」は、「この円柱を真上から見たときに2点が重なる、一致するということと同じ」であることはすぐに分かります。
円柱も平行も一種の「引っかけ」というか、数学的な表現に変換されているだけで、基本は時計算とか旅人算。つまり、「数学的な表現」を読み解けば、ここに書いたような小学生の算数の問題になるわけです。
算数で解こうとすれば難しいのですが、数学の基礎をちゃんと学び取っていれば、誰でも解ける問題です。(問題量が多すぎてじっくり解いている時間がない、というような批判は別。全体の問題量が適切かまでは見ていません。あくまでもこの問題が難しすぎるのかどうかということだけを考察しています)
簡単に言える内容なのに、わざわざ円柱だの平行だのという言い方に変えているのは難問奇問を作為的に作っていてけしからん、という批判が出るかもしれません。しかし、それは「数学的表現とはどういうものか」という基本的なことを学んでいるかどうかを見るにはとてもいい方法です。
例えば、将来、何かの装置を作るとき、このような円筒状の両端で逆方向に違う速度で回るベアリングとか歯車とかの設計をすることがあるかもしれません。そのとき、計算上、円柱を考える必要はないのだ、と分かるかどうかというのはものすごく基本的なことで、技術者や設計者に問われる基礎力です。
そんなことも気がつかないような頭の人に、重要な装置や機械を設計し、運用させることはできません。
ここで話を放射能事故に戻します。
東電や保安院の記者会見を見ていて、多くの人は「この人たちって、難しい入試を突破して、偏差値の高い大学に入って、優秀な成績で卒業してこの仕事に就いたんでしょうに、なんでこんなにバカなのかしら」と不思議に思ったに違いありません。
昨日、たまたまフェイスブックで「長野県の県立高校入試問題における数学の問題が超難問で、受験生が泣いている」という話題を見つけたのですが、すでにネット上では、教科書に載っていないようなこんな難問を出すべきではないという論がたくさん書き込まれているようです。
あげくは、 //県教組では、現行の学習指導要領を逸脱していると判断し、15日になって県教委に抗議し、外部評価を行うよう申し入れた// なんて記事まで出てきました。
バッカじゃなかろか。
そんなとんでもない問題ではないことは、ここに説明したとおり。むしろこれは、 y=ax+b という一次関数の基本さえ理解していれば誰でも解ける「いい問題」なのです。しかも、「数学的表現」を一般的な意味合いに読み替えて直観的に把握する能力も問われています。
この問題を評して「数学の問題というよりは国語の問題」と言っている人がいましたが、ある意味そうかもしれません。
つまり、数学とはどういう学問なのか、その「精神」を知らせることが本当の教育ではないのか、というテーマを表現しているのですね。
数学って、一見難しいように思えても、噛み砕いて考えればどうということのないことも多いんだよ。しかも、一度数式を作ってしまうと後はあてはめるだけで簡単に答えが出てくるから便利なんだよ、ということを教えている。
しっかりした教育哲学を持った人が作った問題だと思います。
数学が苦手な生徒でも、頭を使えば必ず解けるということがすごく重要です。その意味において、この問題はとてもいい問題なのです。
ちなみに僕は高校生ですでに数学を捨ててしまい、大学は数学が入試科目にない私立文系のみを受けました。
実は、この問題を解いているときも、y=ax+b なんて忘れていたし、このaがマイナスになるとグラフが右下がりのグラフになるという超基本的なことさえすっかり忘れていました。問題を解きながら、そういえばそんなことを教わっていた気がするなあ……という程度の記憶がゆるやかに甦ってきてちょっと嬉しくなったりもしました。理系の人からはバカにされそうですが、ほんとにそれほどひどい落ちこぼれなのです。
そんな僕でさえ、考えれば解けるのですから、ましてや現役で数学を学んでいた中学生が解けないはずはありません。
教科書の例題を丸暗記して定期試験で点を取るタイプの生徒、定期試験の点を取る要領だけを身につけた生徒は面食らうかもしれません。しかし、そういう生徒、「想定内の問題だけ勉強すればいい」という根性の生徒が点を取れるようなパターン化した試験問題こそ、官僚バカ、学者バカ、バカ政治家たちを量産する、悪い試験問題といえるでしょう。
頭の使い方を鍛えないで、「想定外でした」なんていう嘘を平気でつくような図太さだけは身につける。日本の将来を背負う子供たちが、そんな大人に育っていくのではたまったものではありません。
この問題を見て、考える前に泣き出すだとか、この後の科目を投げちゃうなんていうのは、数学以前に、人間の芯の強さとか、根性とかが足りないわけで、それもまた問題だと思います。
入試を楽しむくらいの力量、余裕を持ってくれよ。これから先の人生、いっぱい大変なことがあるんだから、この程度のことでめげてたらやっていけないよ、と言いたいのです。
……あ~、何十年ぶりかで数学のエッセンスを楽しませてもらった気分です。この問題の作者に感謝!
もしかして、この問題の作者は、ヤマゲン先生みたいな人かもしれないなあ。
◆小説、狛犬本、ドキュメンタリー……「タヌパックブックス」は⇒こちらから
◆「タヌパックブックス」は⇒

◆コロナで巣ごもりの今こそ、大人も子供も「森水学園」で楽しもう

『介護施設は「人」で選べ』
親を安心して預けられる施設とは? ご案内ページは⇒こちら
『3.11後を生きるきみたちへ 福島からのメッセージ』
(2012/04/20発売 岩波ジュニア新書)…… 3.11後1年を経て、経験したこと、新たに分かったこと、そして至った結論■今すぐご注文できます
立ち読み版は⇒こちら

「狛犬本」の決定版!